Introduction and Motivation

The “Jaffe Wins Above Replacement Score”, aka JAWS, is a widely acknowledged sabermetric methodology for identifying Hall of Fame worthy players. It is defined, simply, as the average of the player’s career wins above replacement (WAR) with their ‘peak 7 year WAR,’ the total WAR achieved over their best 7 year stretch. This JAWS index is then compared to the average JAWS index of players already in the Hall of Fame, for their position. A player is deemed ‘worthy’ of the Hall of Fame if their JAWS index meets this threshold.

This calculation seems very simple, but is not that easy to calculate efficiently and cleanly. This post goes through that process and explains, step-by-step, the R code necessary. I also share a bunch of tips and tricks that could greatly help your R workflow.

We’re going to need a few packages, so install them if you haven’t yet: Lahman, dplyr, magrittr, readr, and ggplot2.

Data collection and exploration

First, we need to get data about these baseball players. Luckily, a number of R packages collect data about MLB players and make it easily accessible.

We use a package openWARData, used as inputs to the Open WAR standard as our source of WAR information. This package collects WAR information from the leading WAR implementations, FanGraphs and Baseball Reference.¹ For this post, we will only consider Baseball Reference WAR calculations.

Using that data, we can take a quick look at the underlying data (10 randomly sampled rows).

playerId	yearId	stintId	PA	runs_position	rRAA_bat	rRAA_field	BFP	rRAA_pitch	TPA	rRAR	rRAA	rRepl	rWAR	teamId
mauchge01	1948	2	166	2.5	-1.1	0.5	NA	NA	166	3.5	-3.1	-6.6	0.33	CHC
tudorjo01	1981	1	0	0.1	0.1	0.1	331	-6.487	331	0.293	-6.387	-6.68	-0.03	BOS
conroti01	1987	1	17	0.06	-1.6	0.1	188	-5.658	205	-3.422	-7.258	-3.836	-0.39	STL
niemabo01	1952	1	533	-5.72	5.6	-5.7	NA	NA	533	21.9	5.6	-16.3	2.24	SLB
bergmda01	1988	1	333	-6.95	1.8	-5.2	NA	NA	333	14.9	3.5	-11.4	1.51	DET
butchma01	1938	1	27	0	0.4	0	355	-27.023	382	-20.278	-26.623	-6.345	-1.91	BRO
tablepa01	1991	1	222	-6.42	-17.5	-4.8	NA	NA	222	-8	-15.9	-7.9	-0.91	TOR
stratmo01	1937	1	65	0	-1.1	0	650	33.972	715	52.123	32.872	-19.251	4.81	CHW
duryeje01	1890	1	123	-0.1	3.7	-0.1	0	10.47	123	46.023	14.17	-31.853	4.29	CIN
covenja01	1903	1	14	0.23	-1.7	0.2	NA	NA	14	-1.3	-1.7	-0.4	-0.13	STL

There’s plenty of information here, but we only need so much. We can narrow this down to only player-year pairs of rWAR. That is, the rWAR achieved by each player in each year.

war_short <- war_dat %>%
  group_by(playerId) %>%
  select(playerId, yearId, rWAR) %>% ungroup

playerId	yearId	rWAR
cabreor01	2000	-0.91
germaju01	2010	0.31
almonbi01	1986	0.26
venafmi01	2002	0.02
hasslan01	1978	-0.5
boddimi01	1982	0.3
campbgi01	1936	1.67
mclemma01	1996	4.26
letchch01	1941	-0.08
riverbo01	1976	0.39

Part 1: JAWS Calculation

The first component of the JAWS method is the career WAR. We can easily visualize the distribution via the ggplot2 package. The following commands are all we need to do, in English and translated into R:

1. Start with the above dataset war_short
2. Group by player, because we are concerned with the characteristics of each individual player
3. Filter our dataset to only include those players with more than 7 years played.²
4. Since we’re at the individual level, we can sum up the WAR for each player.
5. Call ggplot2, and focus on the total_war variable
6. Create a histogram of the data
7. Cut the data off at 0 and 50 WAR, and ‘squish’ the results into range.
8. Label our axes and give the plot a title.

war_career <- war_short %>% 
  group_by(playerId) %>%
  filter(n() >= 7) %>%
  summarize(total_war = round(sum(rWAR), 2))

war_career %>%
  ggplot(aes(total_war)) +
  geom_histogram(bins = 25) + 
  scale_x_continuous(limits = c(-5, 50), oob = scales::squish) +
  xlab("rWAR") + ylab("Count") + ggtitle("Distribution of Career WAR")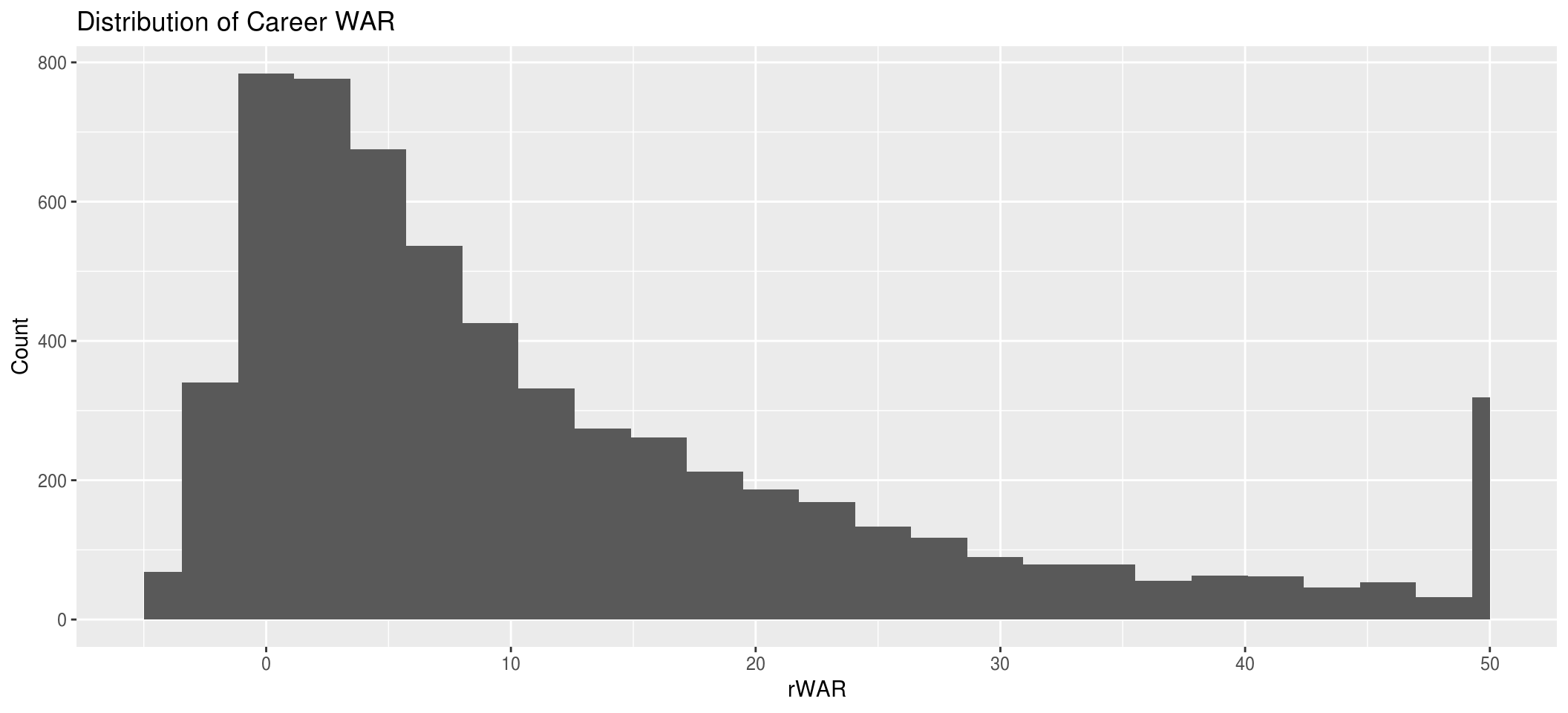

This data looks like what we’d expect - a lot of players who have total WAR close to 0, denoting that they’ve performed at a replacement level, and a significant chunk of people who’ve earned more than 50 WAR.

Calculating total career WAR is easy and quick, and might feel like a good metric to use overall. However, high performers according to career WAR require longevity in the major leagues, and punishes players who had a number of very good years, but not the longest career. JAWS attempts to correct for this by calculating peak WAR.

Our general process is as follows:

1. Begin with the same dataset as above
2. Group by player and year, so even if a player is traded or went down to the minors, their season is counted as one.
3. For each player-year pairing, sum up the WAR for that year.
4. Ungroup and group by player instead, since we want to now ‘move’ across years.
5. We need to do a rolling window sum. This step is pretty tricky, so I go more into depth in the appendix.³
6. We group by player again and determine the highest peak WAR for each player.

war_peak <- war_short %>%
  group_by(playerId, yearId) %>%
  summarize(rWAR = sum(rWAR)) %>%
  ungroup %>% group_by(playerId) %$%
  data.frame(playerId, yearId, 
             roll_war = slide_apply(data = rWAR, window = 7,
                                    fun = sum, na.rm = T)) %>%
  group_by(playerId) %>%
  summarize(peak_war = max(roll_war, na.rm = T))

playerId	peak_war
aardsda01	2.2
aaronha01	58.85
aaronto01	19.25
aasedo01	12.96
abadan01	2.27
abadfe01	2.59
abadijo01	3.49
abbated01	9.08
abbeybe01	9.16
abbeych01	2.95

We can take this data and plot the distribution of the peak WAR values. This distribution looks very similar to our above one, but with way fewer values that are out of bound to the right.

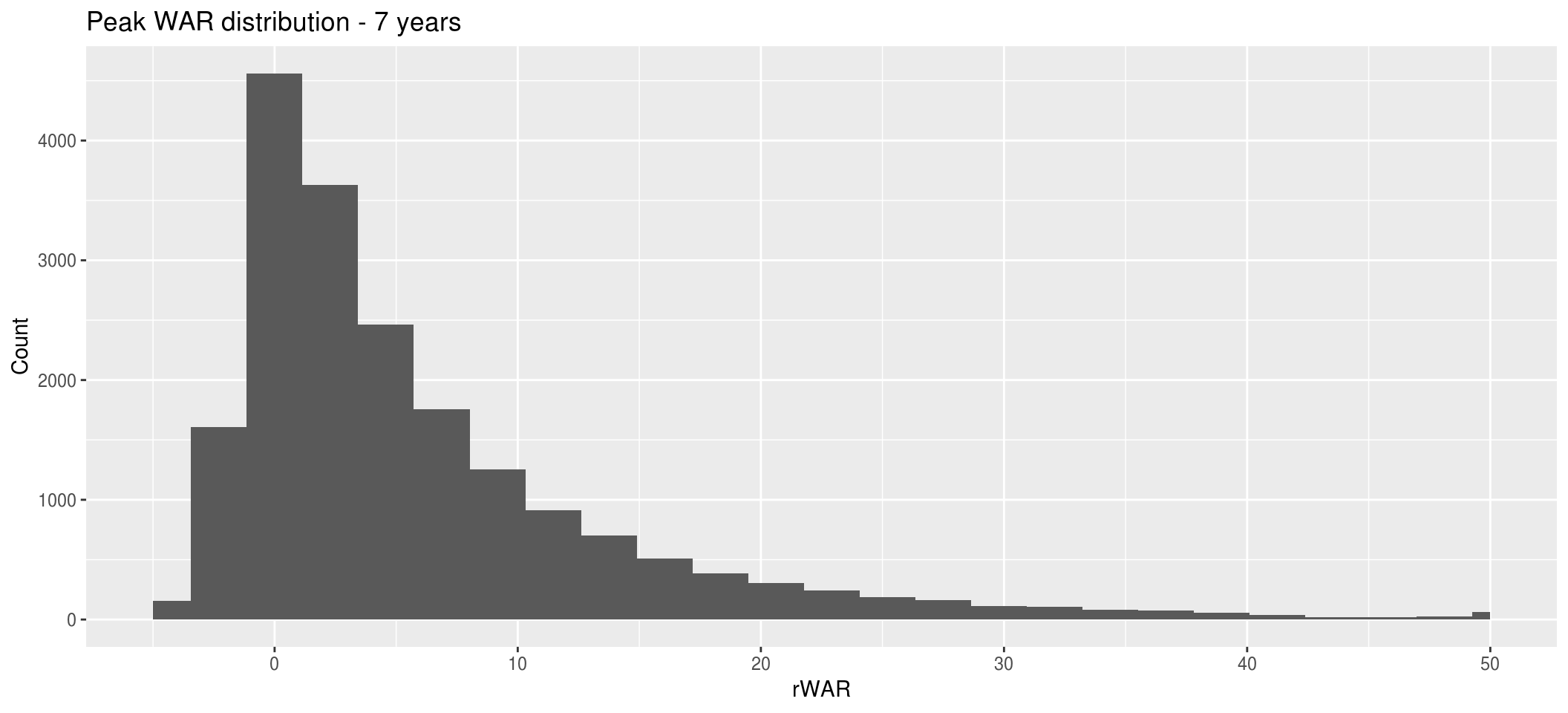
Now, we have two data frames with career WAR and peak WAR. We can merge them by joining on player ID to get the following output:

war_merge <- left_join(war_career, war_peak, by = "playerId")

playerId	total_war	peak_war
aardsda01	1.87	2.2
aaronha01	142.57	58.85
aaronto01	-2.79	19.25
aasedo01	15.26	12.96
abadfe01	3.04	2.59
abbated01	8.59	9.08
abbotgl01	5.67	6.15
abbotji01	19.88	22.64
abbotku01	0.57	4.83
abbotpa01	4.72	6.94

Then, calculating the JAWS index is easy:

war_merge %<>%
  mutate(JAWS = (total_war + peak_war)/2)

playerId	total_war	peak_war	JAWS
aardsda01	1.87	2.2	2.035
aaronha01	142.57	58.85	100.71
aaronto01	-2.79	19.25	8.23
aasedo01	15.26	12.96	14.11
abadfe01	3.04	2.59	2.815
abbated01	8.59	9.08	8.835
abbotgl01	5.67	6.15	5.91
abbotji01	19.88	22.64	21.26
abbotku01	0.57	4.83	2.7
abbotpa01	4.72	6.94	5.83

Part 2: Comparisons

Certain positions are known to emphasize defensive ability over offensive stats, which generally reduces their WAR numbers. Most commonly, teams consider the value of a shortstop or catcher to come from their defensive ability, not dropping pitches or covering a lot of ground acrobatically, rather than their bat. The flip side is that corner outfielders and first basemen have easier jobs, and so demand greater offensive output.

The JAWS methodology accounts for position-wide disparities by comparing each player to only those Hall of Fame players who played the same position. We can try to do the same.

The Lahman and Baseball Reference datasets don’t provide us with a position label for each player, which makes sense because players often play different positions and often shift positions throughout their career. We do our best to classify each player here by calculating the number of games played by each player at each position, and then taking the position where they played the max.

1. We start with the Lahman::Fielding table, which includes fielding appearances by each player and the position at which they appeared.
2. We limit the number of columns to player, JAWS score, year, position, and games played
3. We group by the player and the positions they’ve played
4. We summarize by summing up the games played at each position.
5. We then group at the player level, and select only rows with the most games played at the position. In effect, we select the position most played.

pos_data <- Lahman::Fielding %>%
  group_by(playerID, POS) %>%
  summarize(gp_pos = sum(G)) %>%
  group_by(playerID) %>%
  filter(gp_pos == max(gp_pos)) %>% 
  ungroup

war_pos <- war_merge %>% 
  left_join(pos_data, by = c("playerId" = "playerID"))

playerId	total_war	peak_war	JAWS	POS	gp_pos
aardsda01	1.87	2.2	2.035	P	331
aaronha01	142.57	58.85	100.71	OF	2760
aaronto01	-2.79	19.25	8.23	1B	232
aasedo01	15.26	12.96	14.11	P	448
abadfe01	3.04	2.59	2.815	P	315
abbated01	8.59	9.08	8.835	2B	419
abbotgl01	5.67	6.15	5.91	P	248
abbotji01	19.88	22.64	21.26	P	263
abbotku01	0.57	4.83	2.7	SS	349
abbotpa01	4.72	6.94	5.83	P	162

Now we want to know if a player was inducted into the Hall of Fame. First, we get the dataframe of Hall of Fame inductions. This uses the Lahman::HallOfFame table, which contains all votes for the Hall of Fame. Note that some players are not inducted, so we need to check if they’ve ever been inducted. In the data, the inducted variable shows up as ‘Y’ or ‘N’; the easiest way to do this is to check if any instance of inducted for each player is ‘Y’.

## Observations: 4,156
## Variables: 9
## $ playerID    <chr> "cobbty01", "ruthba01", "wagneho01", "mathech01", ...
## $ yearID      <int> 1936, 1936, 1936, 1936, 1936, 1936, 1936, 1936, 19...
## $ votedBy     <chr> "BBWAA", "BBWAA", "BBWAA", "BBWAA", "BBWAA", "BBWA...
## $ ballots     <int> 226, 226, 226, 226, 226, 226, 226, 226, 226, 226, ...
## $ needed      <int> 170, 170, 170, 170, 170, 170, 170, 170, 170, 170, ...
## $ votes       <int> 222, 215, 215, 205, 189, 146, 133, 111, 105, 80, 7...
## $ inducted    <fctr> Y, Y, Y, Y, Y, N, N, N, N, N, N, N, N, N, N, N, N...
## $ category    <fctr> Player, Player, Player, Player, Player, Player, P...
## $ needed_note <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA...

hof <- Lahman::HallOfFame %>%
  group_by(playerID) %>%
  summarize(inducted = any(inducted == "Y"))

playerID	inducted
aaronha01	TRUE
abbotji01	FALSE
adamsba01	FALSE
adamsbo03	FALSE
adamssp01	FALSE
ageeto01	FALSE
aguilri01	FALSE
akerja01	FALSE
alexado01	FALSE
alexape01	TRUE

We can join this data against our above dataset to get our final table, with all the data we need.

jaws_final <- war_pos %>% 
  left_join(hof, by = c("playerId" = "playerID")) %>%
  tidyr::replace_na(replace = list(inducted = F)) %>%
  select(playerId, JAWS:inducted)

playerId	JAWS	POS	gp_pos	inducted
aardsda01	2.035	P	331	FALSE
aaronha01	100.71	OF	2760	TRUE
aaronto01	8.23	1B	232	FALSE
aasedo01	14.11	P	448	FALSE
abadfe01	2.815	P	315	FALSE
abbated01	8.835	2B	419	FALSE
abbotgl01	5.91	P	248	FALSE
abbotji01	21.26	P	263	FALSE
abbotku01	2.7	SS	349	FALSE
abbotpa01	5.83	P	162	FALSE

Now, we want to see the average for each position’s Hall of Famers.

jaws_hof <- jaws_final %>%
  filter(inducted == TRUE) %>%
  group_by(POS) %>%
  summarize(count = n(), avg = mean(JAWS))

POS	count	avg
1B	23	52.2469565
2B	22	49.7525
3B	15	49.689
C	19	37.5981579
OF	69	51.2357971
P	69	58.0013043
SS	23	49.0973913

Conclusion

We’ve examined a real world ‘sabermetric,’ the JAWS index, and replicated its calculations in R.

How does our JAWS index compare to the listed Baseball Prospectus JAWS?

##    POS JAWS
## 1    C 42.6
## 2   1B 51.4
## 3   2B 53.8
## 4   3B 55.0
## 5   SS 50.7
## 6   LF 53.5
## 7   CF 58.3
## 8   RF 53.6
## 9   SP 43.5
## 10  RP 23.3

Our calculation is close. Some of the differences can be attributed to the above BP data being outdated (it was calculated in 2012), as well as possibly mislabelled player positions.

Appendix